Module 2b - Automatic differentiation

Table of Contents

Automatic differentiation

0:00 Recap
0:40 A simple example (more in the practicals)
3:44 Pytorch tensor: requires_grad field
6:44 Pytorch backward function
9:05 The chain rule on our example
16:00 Linear regression
18:00 Gradient descent with numpy...
27:30 ... with pytorch tensors
31:30 Using autograd
34:35 Using a neural network (linear layer)
39:50 Using a pytorch optimizer
44:00 algorithm: how automatic differentiation works

Slides and Notebook

• Automatic differentiation: a simple example static notebook, code (GitHub) in colab

• notebook used in the video for the linear regression. If you want to open it in colab

• backprop slide (used for the practical below)

Quiz

To check your understanding of automatic differentiation, you can do the quizzes

Practicals

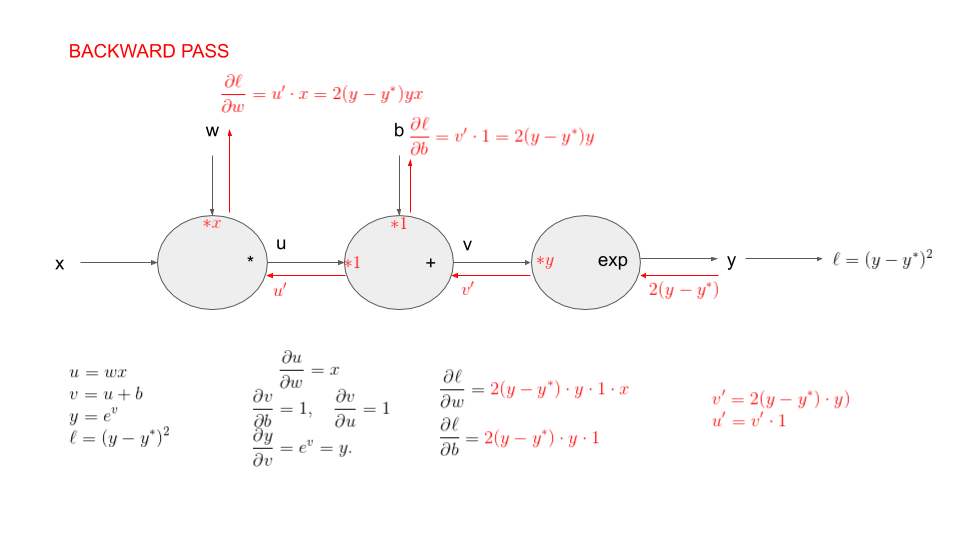
• practicals in colab Coding backprop.

Challenge

Adapt your code to solve the following challenge:

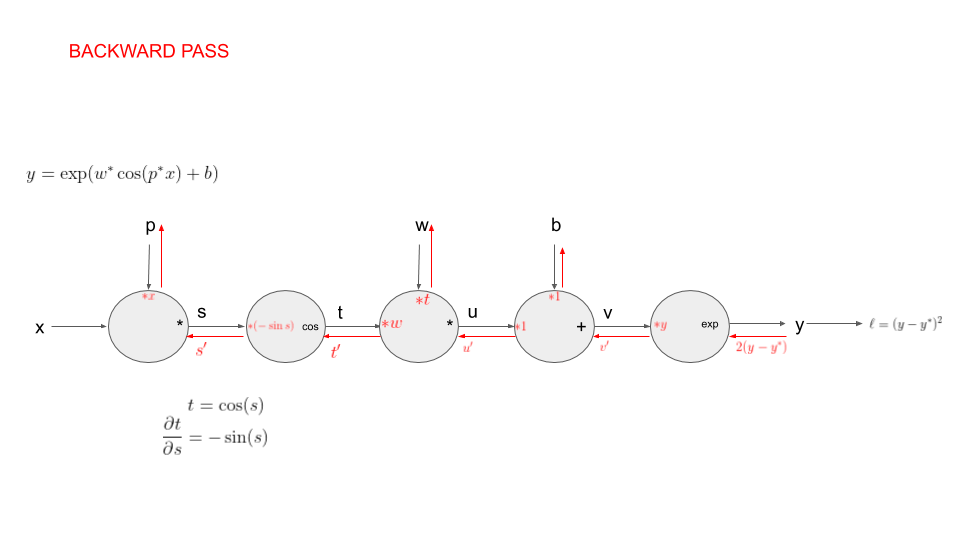
Some small modifications:

• First modification: we now generate points $(x_t,y_t)$ where $y_t= \exp(w^*\cos(x_t)+b^*)$, i.e $y^*_t$ is obtained by applying a deterministic function to $x_t$ with parameters $w^*$ and $b^*$. Our goal is still to recover the parameters $w^*$ and $b^*$ from the observations $(x_t,y_t)$.

• Second modification: we now generate points $(x_t,y_t)$ where $y_t= \exp(w^*\cos(p^*x_t)+b^*)$, i.e $y^*_t$ is obtained by applying a deterministic function to $x_t$ with parameters $p^*$, $w^*$ and $b^*$. Our goal is still to recover the parameters from the observations $(x_t,y_t)$.

Bonus:

• JAX implementation of the linear regression notebook in colab see Module 2c for more details.

Edit this page on Last modified: May 30, 2023. Website built with Franklin.jl and the Julia programming language.