Module 12 - Attention and Transformers

Table of Contents

Attention with RNNs

The first attention mechanism was proposed in Neural Machine Translation by Jointly Learning to Align and Translate by Dzmitry Bahdanau, Kyunghyun Cho, Yoshua Bengio (presented at ICLR 2015).

The task considered is English-to-French translation and the attention mechanism is proposed to extend a seq2seq architecture by adding a context vector $c_i$ in the RNN decoder so that, the hidden states for the decoder are computed recursively as $s_i = f(s_{i-1}, y_{i-1}, c_i)$ where $y_{i-1}$ is the previously predicted token and predictions are made in a probabilist manner as $y_i \sim g(y_{i-1},s_i,c_i)$ where $s_i$ and $c_i$ are the current hidden state and context of the decoder.

Now the main novelty is the introduction of the context $c_i$ which is a weighted average of all the hidden states of the encoder: $c_i = \sum_{j=1}^T \alpha_{i,j} h_j$ where $T$ is the length of the input sequence, $h_1,\dots, h_T$ are the corresponding hidden states of the decoder and $\sum_j \alpha_{i,j}=1$. Hence the context allows passing direct information from the 'relevant' part of the input to the decoder. The coefficients $(\alpha_{i,j})_{j=1}^T$ are computed from the current hidden state of the decoder $s_{i-1}$ and all the hidden states from the encoder $(h_1, \dots, h_T)$ as explained below (taken from the original paper):

PyTorch implementation

In Attention for seq2seq, you can play with a simple model and code the attention mechanism proposed in the paper. For the alignment network $a$ (used to define the coefficient $\alpha_{i,j} = softmax_{j}(a(s_{i-1},h_j))$), we take a MLP with $\tanh$ activations.

You will learn about seq2seq, teacher-forcing for RNNs and build the attention mechanism. To simplify things, we do not deal with batches (see Batches with sequences in Pytorch for more on that). The solution for this practical is provided in Attention for seq2seq- solution

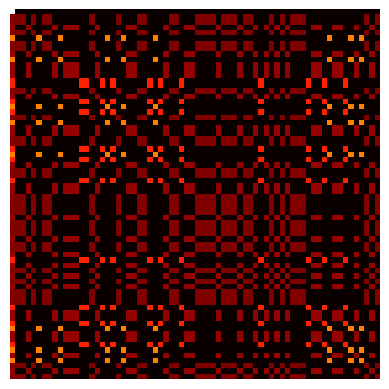
Note that each $\alpha_{i,j}$ is a real number so that we can display the matrix of $\alpha_{i,j}$'s where $j$ ranges over the input tokens and $i$ over the output tokens, see below (taken from the paper):

(Self-)Attention in Transformers

We now describe the attention mechanism proposed in Attention Is All You Need by Vaswani et al. First, we recall basic notions from retrieval systems: query/key/value illustrated by an example: search for videos on Youtube. In this example, the query is the text in the search bar, the key is the metadata associated with the videos which are the values. Hence a score can be computed from the query and all the keys. Finally, the matched video with the highest score is returned.

We see that we can formalize this process as follows: if $Q_s$ is the current query and $K_t$ and $V_t$ are all the keys and values in the database, we return

where $\sum_{t=1}^T\text{softmax}_{t}(\text{score}(Q_s, K_t))=1$.

Note that this formalism allows us to recover the way contexts were computed above (where the score function was called the alignment network). Now, we will change the score function and consider dot-product attention: $\text{score}(Q_s, K_t) = \frac{Q_s^TK_t}{\sqrt{d}}$. Note that for this definition to make sense, both the query $Q_s$ and the key $K_t$ need to live in the same space and $d$ is the dimension of this space.

Given $s$ inputs in $\mathbb{R}^{d_{\text{in}}}$ denoted by a matrix $X\in \mathbb{R}^{d_{\text{in}}\times s}$ and a database containing $t$ samples in $\mathbb{R}^{d'}$ denoted by a matrix $X'\in \mathbb{R}^{d'\times t}$, we define:

Now self-attention is simply obtained with $X=X'$ (so that $d'=d_{\text{in}}$) and $d_{\text{in}} = d_{\text{out}} = d$. In summary, self-attention layer can take as input any tensor of the form $X \in \mathbb{R}^{d\times T}$ (for any $T$) has parameters:

and produce $Y \in \mathbb{R}^{d\times T}$ (with same $d$ and $t$ as for the input). $d$ is the dimension of the input and $k$ is a hyper-parameter of the self-attention layer:

with the convention that $X_t\in \mathbb{R}^d$ (resp. $Y_s\in \mathbb{R}^d$) is the $t$-th column of $X$ (resp. the $s$-th column of $Y$). Note that the notation $\text{softmax}_{t}(.)$ might be a bit confusing. Recall that $\text{softmax}$ is always taking as input a vector and returning a (normalized) vector. In practice, most of the time, we are dealing with batches so that the $\text{softmax}$ function is taking as input a matrix (or tensor) and we need to normalize according to the right axis! Named tensor notation see below deals with this notational issue. I also find the interpretation given below helpful:

Mental model for self-attention: self-attention interpreted as taking expectation

where the mappings $q(.), k(.)$ and $v(.)$ represent query, key and value.

Multi-head attention combines several such operations in parallel, and $Y$ is the concatenation of the results along the feature dimension to which is applied one more linear transformation.

Transformer block

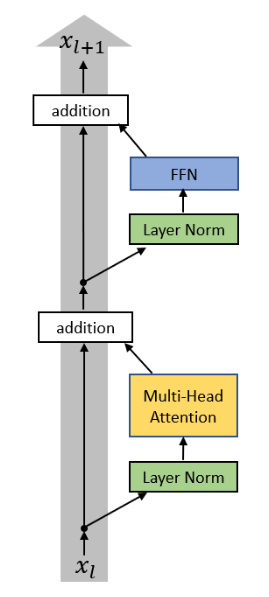
To finish the description of a transformer block, we need to define two last layers: Layer Norm and Feed Forward Network.

The Layer Norm used in the transformer block is particularly simple as it acts on vectors and standardizes it as follows: for $x\in \mathbb{R}^d$, we define

and then the Layer Norm has two parameters $\gamma, \beta\in \mathbb{R}^d$ and

where we used the natural broadcasting rule for subtracting the mean and dividing by std and $\cdot$ is component-wise multiplication.

A Feed Forward Network is an MLP acting on vectors: for $x\in \mathbb{R}^d$, we define

where $W_1\in \mathbb{R}^{d\times h}$, $b_1\in \mathbb{R}^h$, $W_2\in \mathbb{R}^{h\times d}$, $b_2\in \mathbb{R}^d$.

Each of these layers is applied on each of the inputs given to the transformer block as depicted below:

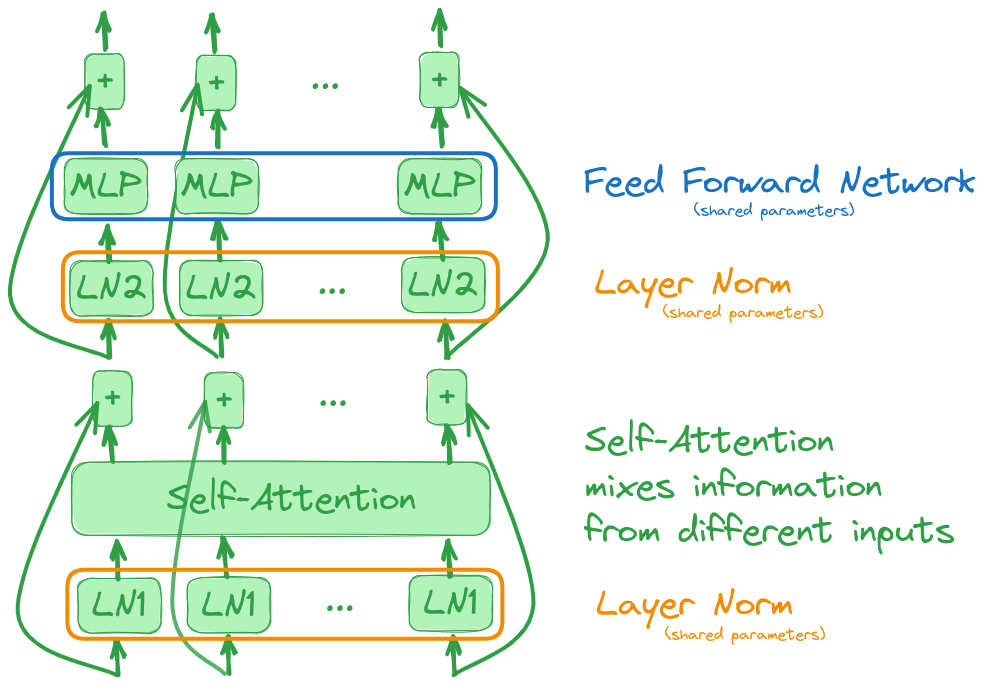
Note that this block is equivariant: if we permute the inputs, then the outputs will be permuted with the same permutation. As a result, the order of the input is irrelevant to the transformer block. In particular, this order cannot be used. The important notion of positional encoding allows us to take order into account. It is a deterministic unique encoding for each time step that is added to the input tokens.

Transformers using Named Tensor Notation

In Transformers using Named Tensor Notation, we derive the formal equations for the Transformer block using named tensor notation.

Hacking a simple Transformer block

Now is the time to have fun building a simple transformer block and to think like transformers (open in colab).

Edit this page on Last modified: May 30, 2023. Website built with Franklin.jl and the Julia programming language.